Nicholas of Cusa and the Infinite

Thomas J. McFarlane

23 March 1999

Revised and edited for the web March 2004

ABSTRACT: Nicholas of Cusa (1401-64) was a philosopher and theologian whose writings influenced the development of Renaissance mathematics and science. The first part of this paper will trace the historical development in the West of thought about the Infinite prior to the time of Nicholas of Cusa. The second part of the paper will discuss his philosophy as presented in his major work, On Learned Ignorance. The third part of the paper will then examine the subsequent development of thought about the Infinite and the ways in which Nicholas of Cusa influenced mathematics and science.

Preface: A Meditation on the Infinite

According to the movement of reason, plurality or multitude is opposed to unity. Hence, it is not a unity of this sort which properly applies to God, but the unity to which neither otherness nor plurality nor multiplicity is opposed. This unity is the maximum name enfolding all things in its simplicity of unity, and this is the name which is ineffable and above all understanding.[1]

What is the Infinite? To define it as other than the finite is to set the infinite apart from the finite, and thereby limit it. To define the infinite, therefore, is to make it definite, and no longer infinite. In fact, to say anything at all of the Infinite, is to actually say nothing about the true Infinite. Like the Tao, the Infinite that can be named is not the true Infinite. The Infinite, then, is ineffable. …Or is it? If we think that the Infinite is ineffable, we have once again defined it by distinguishing it from what is not ineffable. The Infinite is so utterly ineffable that we cannot even say that it is ineffable. Even this, however, is saying too much.

The Infinite is paradoxical and contradictory. Yet, while it cannot be defined or represented in rational terms, it is nevertheless profoundly meaningful. The Infinite is a numinous reality that has flooded the human mind with awe and inspiration for thousands of years. Throughout history, the intuition of the Infinite has been known by equally profound and paradoxical terms: the Absolute, the One, the Unconditioned, the Unlimited, the Indivisible, and the Indefinite. Philosophers have identified it with Reality and Truth. Mystics have called it God, Brahman, Allah, and Tao. On the one hand, the Infinite inspires a sense of a potential for limitless expansion beyond any finite bound. On the other hand, the Infinite also inspires a sense of an actual completeness comprehending everything without any exclusion whatsoever. The former is a view from the finite upward toward the unattainable and incomprehensible infinite, while the latter is an incomprehensible view from the infinite downward toward the finite that is identical with the infinite. As we will see, a dialectical play between these two aspects of our intuition of the Infinite reveals a process of actualization of the Infinite in the history of Western thought.

A History of the Infinite Before 1400

The concept of infinity first appears in the West with Anaximander of Miletus (c. 610-546 BC), who proposed that the principle of all things is that which is without any limit (peras). This limitless principle is thus called the not-limited (to aperion). Because it is without any limit, all opposites are transcended in to aperion, and all conflict between created things is reconciled. Whereas Anaximander viewed to aperion as good, Pythagoras (born c. 570 BC) viewed to aperion as abhorrent, because it is incomprehensible, indefinite, and lacks the harmony and beauty that is present only in the cosmos. Pythagoras taught that all things are number, and that the cosmos is created and governed by comprehensible and definite numerical principles. In the Pythagorean cosmogenesis, the derivation of the multiplicity of things in the world from an original unity is identical to the derivation of the numbers from the numerical unit, one. The Pythagoreans saw in all things combinations of eternal principles, such as Limit and Unlimited, One and Many, At Rest and In Motion. This Pythagorean vision, which sees the material world of becoming as imitating the mathematical world of being, provided the seminal insight at the foundation of Western science, both ancient and modern. A problem with the Pythagorean vision, however, was discovered by the Pythagoreans themselves. If the entire cosmos is constituted and ordered by whole numbers and their proportions, then everything must be comprehensible in terms of integral proportions of other things. This thesis, however, was shown to be false when it was mathematically demonstrated that the length of the diagonal of a unit square is incommensurate with the lengths of its sides. In modern terms, we might say that the Pythagoreans discovered that the square root of two is not a rational number. The Greeks, however, did not consider geometric magnitudes to be numbers at all. Numbers were discrete integral quantities: 1, 2, 3, etc. that had arithmetic properties of being even, odd, prime and so on. Geometric magnitudes, on the other hand, were continuous spatial objects for which concepts of even and odd had no meaning. Because of the impossibility of expressing geometric magnitudes in terms of arithmetic quantities, the Greeks considered arithmetic and geometry to be fundamentally distinct. This schism in mathematics between the continuous magnitudes of geometry and the discrete quantities of arithmetic was one manifestation of the profound problem of relating the Unlimited and the Limited, the Infinite and the finite. The indefinite and incomprehensible to aperion was somehow present in the continuous magnitudes of geometry, and the discrete numbers and their ratios could not represent them.

Zeno developed several famous paradoxes that illustrate the incompatibility between the discrete and continuous. For example, in one variant of Zeno’s thought experiments, it is shown that a flying arrow cannot hit its target since it must first travel half way to the target, and then half of the remaining distance, and so on.

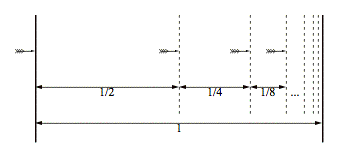
In arithmetic terms, if the total distance to the target is 1, then the arrow must first travel a distance of 1/2, then a distance of 1/4, then a distance of 1/8, and so on. After a number n of such steps, the total distance traveled by the arrow will be 1/2 + 1/4 + 1/8 + … + 1/2ⁿ = 1 – 1/2ⁿ. No matter how large n is, however, this sum will always be less than the total distance to the target, since for any value of n, 1 – 1/2ⁿ < 1. Thus, the arrow can never hit its target.

Zeno used this thought experiment to demonstrate the contradictions inherent in attempting to understand the unity of continuous motion in terms of a diversity of discrete comprehensible steps. Neither Zeno nor the Pythagoreans, however, resolved this paradox. Thus, the tension between Unlimited and Limited continued to play out in the dialectic of Western thought.

One of the important ways in which the dialectic between Infinite and finite played out in philosophic thought is in the attempts to understand the relationship between Being and Becoming. In addition to the problem of explaining how the finite world of becoming arises from the Infinite world of Being, there is the additional problem of understanding how becoming can be related to being. Heraclitus taught that the impermanent flux of becoming implied that all opposites are united in One. Parmenides, like Heraclitus, affirmed the One but emphasized the reality of the One by arguing that change and plurality are impossible to begin with. Thus, the Pythagorean realm of static being is fundamentally incompatible with the impermanence of existing things. Neither Heraclitus nor Parmenides, however, provided an entirely satisfactory philosophical solution to the problem.

A compelling synthesis of Being and Becoming, Limited and Unlimited, One and Many, was provided by Plato in his dialogues, most notably in his Parmenides. With his theory of Forms and the notion of participation, Plato provided an essentially Pythagorean solution to the problem of how the Limited and Unlimited are related. In a naive understanding of the forms, they are isolated, static patterns set in contrast with the changing phenomena of a sensory world. In a more subtle understanding of Plato’s theory of Forms, however, they are recognized as interpenetrating principles that are not other than their own instantiations. The realms of being and becoming do not correspond to separate realms of forms and sensible objects. Instead, being and becoming are both implicit in the nature of both the forms and sensible objects. The Limited and Unlimited, therefore, are coexisting principles that are not fundamentally opposed to one another. A large part of the significance of Plato’s contribution can be understood in terms of his synthesis of the Infinite with the finite in a single body of thought that encompasses them both and provides a way to understand their relationship to each other.

Based on the paradoxes of the infinite discovered by Zeno and others, Aristotle rejected the notion that the infinite could be in any way actual, and proposed instead that the Infinite could only be a potential. Aristotle, in other words, rejected the Infinite as an actual existing reality. In Aristotle’s view, for example, the whole numbers are potentially infinite because there is no limit to how high one can count. The whole numbers are not actually infinite, however, because no matter how high one counts, one has only counted up to some finite number. One can never actually count to infinity. In addition, Aristotle rejected the actual existence of the continuum. Thus, according to Aristotle, the arrow does reach the target because space is not actually infinitely divided. In providing this solution to the paradoxes of motion, however, Aristotle implicitly rejects the foundations of geometry, which assumes the existence of the continuum. This problem with Aristotle’s account of the infinite, however, did not prevent his ideas from having widespread influence for many centuries.

Using Aristotle’s idea of the potential infinite, the Greek mathematician Eudoxus (408-355 BC) provided the seed for what was to become calculus two thousand years later. Eudoxus’ method of exhaustion was extensively used by Archimedes (287-212 BC) to arrive at arithmetic formulas pertaining to geometric figures. For example, he was able to derive a formula for the area of a circle as follows. Consider a regular polygon with n sides. Inscribe within the polygon a circle, and inscribe within the circle another polygon with n sides.

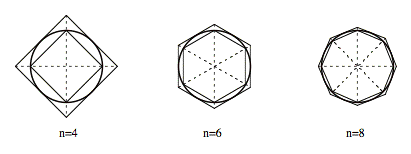
Now notice that both polygons approach the shape of the circle as the number of sides, n, becomes larger. Thus, for large values of n, the areas of the two polygons become very close to the area of the circle. Notice also that the area of the circle is always between the area of the smaller polygon and the area of the larger polygon. The area of the circle can thus be found with any desired precision by selecting a sufficiently large value of n and calculating the areas of the two polygons. This method, however, does not provide a precise value for the area of the circle. To arrive at a precise formula for the actual area of the circle, one would need to take n equal to infinity. But this would require one to add up an infinite number of triangles, which is impossible. Moreover, each triangle would have one side equal to zero, resulting in an area of zero. The areas of the triangles would thus add up to zero. Eudoxus’ method of exhaustion, therefore, involves contradictions and paradoxes if one applies it to the actual infinite. His method does not allow one to precisely calculate certain continuous magnitudes, or to understand the Infinite in finite terms. It only provides a technique for performing approximate calculations of finite quantities that approximate continuous magnitudes. Although Eudoxus’ technique was a practical success, it did not solve the more fundamental problems of infinity. For example, if there is no actual infinity, how are we to understand the existence of the infinite continuum in geometry?

Plotinus (205 – 270 CE), who drew heavily upon the philosophy of Plato, is the founder of what is now known as Neoplatonism. In contrast with Aristotle, Plotinus defended the metaphysical reality of the actual Infinite. While agreeing with Aristotle that there is no actual infinite in the sensible realm, Plotinus asserted the reality of the actual Infinite in a transcendent realm known only through mystical insight. St. Augustine (354-430 CE) was influenced by Plotinus and Plato, and integrated much of Platonism and Neoplatonism with Christianity. The Platonic insight continued to dominate the Christian worldview until St. Thomas Aquinas (1224-1274 CE), whose thought was predominantly Aristotelian. Aquinas, however, parted company with Aristotle by asserting his belief in the metaphysical Infinite, i.e., God. Meanwhile, various mathematical arguments were being developed that helped develop a more subtle understanding of the infinite as represented in geometrical continuity. John Duns Scotus (1266-1308 CE), for example, argued that it was incorrect to think of a circle as being composed of an infinite number of points. Consider two concentric circles of different size.

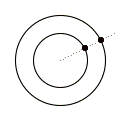
On the one hand, the larger circle must have more points than the smaller circle since it has a longer circumference. On the other hand, because the points along the two circles can be paired up in a one-to-one correspondence, they must have the same number of points. Arguments such as these showed that reasoning about the infinite was not always entirely nonsensical. Although the conclusions may be paradoxical, it suggested that perhaps reason could somehow be applied to infinity without being entirely contradictory. The first person to demonstrate this possibility, and to turn the tide of thought toward the mathematical and philosophical Infinite, was Nicholas of Cusa.

Nicholas of Cusa’s Philosophy

Nicholas of Cusa (1401-1464) was a German cardinal, philosopher, and administrator. For many years he served as papal legate to popes Eugene IV, Nicholas V, and Pius II. In addition to leading an extremely active public life, Nicholas managed to write extensively on a wide variety of juridical, theological, philosophical, and scientific subjects. In his philosophical writings he departed from the prevalent Aristotelian and scholastic doctrines. His first and most famous treatise, On Learned Ignorance (De docta ignorantia), is a mystical discourse on the finite and the infinite. In addition to presenting his important philosophical concepts of learned ignorance and coincidence of opposites, this seminal treatise also contains various bold astronomical and cosmological speculations that depart entirely from traditional doctrines. For example, long before Copernicus, he proposed that the earth is not at the center of the cosmos, and is not at rest. He also argued long before Kepler that the motions of the planets are not circular. These speculations, however, were not based on empirical observations but on metaphysical principles.

Nicholas read widely in various languages and was influenced by Plato and Neoplatonic thinkers such as Plotinus and Proclus. Nicholas also drew inspiration from Dionysius and Meister Eckhart. From Anselm he took the notion of God as ultimate Maximum. From Ramon Lull he took the idea that the infinite is the joining of beginning, middle, and end. The fundamental insight that inspires Nicholas’s thought, however, comes not from his wide learning, but from a mystical illumination in 1437 during a journey home from Constantinople. This gift from God, as he describes the vision, provided him with the key that allowed him to talk about the ineffable, and provided a way of viewing opposites as coincident from the point of view of infinity. According to Nicholas, this logic of infinitude unites opposites, transcends comparison, overcomes limits of discursive reasoning, and goes beyond both positive and negative theology. The profound mystical insight at the heart of Cusa’s logic of infinitude is clearly expressed in the following passage:

In God we must not conceive of distinction and indistinction, for example, as two contradictories, but we must conceive of them as antecedently existing in their own most simple beginning, where distinction is not other than indistinction.[2]

An expression of this insight is Cusa’s idea of coincidence of opposites. Cusa recognized that this idea is an expression of the principle of Incarnation, wherein God’s identification with creation in Jesus coincides with God’s transcendence above all creation. In God the opposites of identity and difference coincide. Thus Nicholas does not present a merely negative theology, but a conception in which the ineffability of the Infinite coincides with its expressibility, in which creation coincides with creator, and transcendent coincides with immanent. As Nicholas writes,

The great Dionysius says that our understanding of God draws near to nothing rather than to something. But sacred ignorance teaches me that that which seems to the intellect to be nothing is the incomprehensible Maximum.[3]

Like Plato, he has a synthetic philosophy that comprehends and integrates opposing streams of thought. Also, Nicholas never attempts to present a consistent and self-contained system of thought. Instead, he remains open to unlimited elaborations of his seminal ideas of learned ignorance and the coincidence of opposites.

Learned ignorance itself is a coincidence of opposites, for it teaches that the more we know our ignorance, the more we attain to true knowledge. Thus, as learned ignorance is perfected, knowledge and ignorance coincide. Using a comparison of the Infinite with the finite, Nicholas explains learned ignorance as follows:

All those who make an investigation judge the uncertain proportionally, by means of a comparison with what is taken to be certain. Therefore, every inquiry is comparative and uses the means of comparative relation. … Hence, the infinite, qua infinite, is unknown; for it escapes all comparative relation.[4]

It is self-evident that there is no comparative relation of the infinite to the finite. … Therefore, it is not the case that by means of likeness a finite intellect can precisely attain the truth about things. … For truth is not something more or something less but is something indivisible. Whatever is not truth cannot measure truth precisely. … For the intellect is to truth as an inscribed polygon is to the inscribing circle.[5]

Here Nicholas introduces a mathematical analogy to explain his metaphysical ideas. Just as the definite polygon cannot measure the continuous circle, our finite minds cannot know the Infinite. All we can know of the Infinite is that we cannot know the Infinite. To the extent that we can understand the Infinite at all, Nicholas argued, we must understand it through the coincidence of opposites. For example, Nicholas taught that, in the Infinite, the circle coincides with the line. He illustrated this paradoxical statement by considering a sequence of circles of larger and larger diameters.

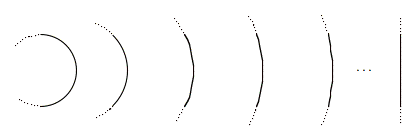
As the circles increase in size, a given length of the circumference is less curved and more similar to a straight line. The infinite circle, therefore, coincides with the line. The actualization of this coincidence of opposites, however, cannot be comprehended by the rational mind. It can only be seen through mystical insight that cannot be consistently expressed in rational terms. Nicholas thus embraces in his thought the opposites of finite and Infinite, arguing for the limits of our rational understanding, while also pointing to an insight that transcends these limits.

Nicholas believed that his doctrine of the coincidence of opposites had implications not just for theology and philosophy, but also for mathematics, physics, and other branches of learning. Boldly contradicting the cosmology of his day, Cusa argued that the cosmos is not bounded by a celestial sphere and does not have the earth, or the sun, at its center:

It is impossible for the world machine to have this sensible earth, air, fire, or anything else for a fixed and immovable center. For in motion there is simply no minimum, such as a fixed center…. And although the world is not Infinite, it cannot be conceived of as finite, since it lacks boundaries within which it is enclosed. … Therefore, just as the earth is not the center of the world, so the sphere of fixed stars is not its circumference.[6]

Because the cosmos is infinitely large, it has no unique center at all, since it can be equally viewed as centered around any point. Nicholas thus introduced the notion of spatial perspective into cosmological thinking:

Since it always appears to every observer, whether on the earth, the sun, or another star, that one is, as if, at an immovable center of things and that all else is being moved, one will always select different poles in relation to oneself, whether one is on the sun, the earth, the moon, Mars, and so forth. Therefore, the world machine will have, one might say, its center everywhere and its circumference nowhere, for its circumference and center is God, who is everywhere and nowhere.[7]

Cusa goes even further to argue that the earth is actually in motion:

The earth, which cannot be the center, cannot lack all motion. In fact, it is even necessary that it be moved in such a way that it could be moved infinitely less.[8]

Anticipating Kepler, Cusa says that the motions of the planets and stars are not circular, and not uniform:

Even if it might seem otherwise to us, neither the sun nor the earth nor any sphere can describe a perfect circle by its motion…nor is a sphere’s or a star’s motion at one moment ever precisely equal to their motion at another.[9]

His cosmological speculations, therefore, did not merely anticipate the Copernican revolution; they went far beyond it. The universe of Cusa was not a heliocentric cosmos with finite size, but a centerless cosmos whose size is infinite.

A History of the Infinite after 1500

Nicholas of Cusa had proposed ideas that appear to anticipate both Copernicus and Kepler. Like Copernicus, he proposed that the earth was not at the center of the cosmos and was in motion. Like Kepler, he proposed that the motions of the planets are not uniform or circular. Nicholas, however, did not base his arguments on empirical data, nor did he develop his ideas into mathematical models that could be tested against experience. Nicholas did not, like Copernicus, show that his ideas could account for astronomical observations with a respectable (although not perfect) amount of accuracy. Nor did Nicholas come even remotely close to Kepler’s discovery that the planets precisely follow elliptical orbits and sweep out equal areas in equal times. Although Nicholas does not deserve credit for these amazing discoveries themselves, his thought dramatically expanded the intellectual horizon of his time, and opened up possibilities of thought that allowed Copernicus and Kepler to make their breakthroughs.

Nicholas of Cusa’s thought also opened up possibilities in mathematics that paved the way for calculus and a mathematics of the continuum. Ever since the Pythagoreans discovered that certain geometrical magnitudes could not be expressed in terms of arithmetic ratios, mathematics had been divided into two incommensurate branches: arithmetic and geometry. This division expressed a fundamental division between the infinite (the geometrical continuum) and the finite (the arithmetic of whole numbers). The Arabs, however, did not let a lack of rigorous theoretical foundations prevent them from freely assuming the existence of irrational numbers and using them in calculations. The use of irrationals was first introduced into Europe around 1200 by Leonardo of Pisa (Fibonacci). Although by Cusa’s time they were in widespread use across Europe, it was not clear in what sense they were actually numbers since they could not be expressed in any definite way, such as by a finite decimal expansion. As Michael Stifel wrote in 1544:

That cannot be called a true number which is of such a nature that it lacks precision…Therefore, just as an infinite number is not a number, so an irrational number is not a true number, but lies hidden in a kind of cloud of infinity.[10]

Indeed, as it would be eventually discovered, the basis for irrational numbers requires a mathematics of the infinite. Thus, as long as infinity was considered absolutely unthinkable, no such mathematics could be found. Through the use of his logic of infinity, and his revival of the actuality of the infinite, Nicholas of Cusa opened the door for these important developments in mathematics.

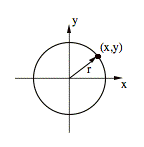
An essential step in the development of modern science was the integration of arithmetic and geometry by René Descartes (1596 – 1650) and Pierre de Fermat (1601-1665). Analytic geometry, as it was called, allowed geometrical objects to be transformed into algebraic equations, and vice versa. This correspondence is made possible by superimposing upon a geometric plane a Cartesian coordinate system that associates to each point P in the plane a unique pair of numbers (x,y). For example, a circle, which is defined geometrically as the set of points equidistant from a central point, can be represented algebraically as the set of coordinates satisfying the equation x²+y²=r², where r is the radius of the circle.

GEOMETRY	ALGEBRA
all points in a plane	all coordinates (x,y)
a unique point P1	a unique pair of coordinates (x1,y1)
a circle with radius r and center P1	(x,y) such that (x-x1)2+(y-y1)2=r2
a line passing through points P1 and P2	(x,y) such that (y-y2)=(x-x2)(y1-y2)/(x1-x2)
the intersection of the above line with the above circle	(x,y) such that both (x-x1)2+(y-y1)2=r2 and (y-y2)=(x-x2)(y1-y2)/(x1-x2)

At the foundation of analytic geometry, however, was the implicit assumption that there actually is a number associated with each point in the continuum of geometric space. As the Pythagoreans had shown, however, there are no such numbers associated with certain geometrical magnitudes. Any attempt to express the coordinates of certain points in numerical form, such as a decimal expansion, results in an infinite sequence. Nevertheless, analytic geometry continued to be used in spite of these unresolved issues at its foundation. They would not be resolved until several hundred years later when a rigorous mathematical foundation for the real numbers was finally provided.

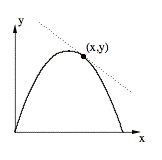
Calculus was a profound mathematical breakthrough with paradoxes of the infinite at its heart. The development of the calculus was motivated in large part by the following problem: given an arbitrary point on a curve, what is the tangent line to the curve at that point? Using analytic geometry, this problem could be translated into an equivalent algebraic problem: given an arbitrary value of one quantity (e.g., time), what is the rate of change (e.g., velocity) of the other quantity (e.g., position)?

Systematic methods for solving this problem were independently devolped by Sir Isaac Newton (1642-1727) and G. W. Leibniz (1646-1716), creating what is now called the calculus. By generalizing Eudoxus’ technique to arbitrary curves and using analytic geometry to apply the principles to algebraic equations, Leibniz and Newton provided powerful techniques for solving many mathematical problems that previously had been impossible to solve. The calculus allowed Newton, for example, to formulate his laws of classical physics and his law of universal gravitation, which profoundly influenced the course of Western history. Here is perhaps the most powerful example of how metaphysical thought about the Infinite has had dramatic consequences in the world.

Despite its remarkable practical success, however, at the heart of the calculus were paradoxes and contradictions. In addition to the fact that it takes for granted the existence of irrational numbers that cannot be represented in any finite way, the calculus also involved nonsensical mathematical manipulations involving infinite sums of infinitesimal quantities. These strange infinitesimals are at once smaller than any positive number, while also not being equal to zero. To make matters worse, the calculus also involved calculating infinite sums of infinitesimals, which mysteriously resulted in finite numbers. Since the calculus worked, it obviously had some truth to it. Yet, it also involved mysterious and incoherent manipulations of infinitesimal quantities, as well as infinite sums. Somehow, Newton and Leibniz had discovered a subtle ‘logic of infinitude’ that allowed them to perform mathematical marvels, without really being able to provide any rigorous account or rational foundation for their methods. Their techniques involved inconsistencies because Newton and Leibniz, following in Cusa’s footsteps, granted actual existence to the infinitely large and infinitely small, and by admitting that an infinite progression can result in an actual limit.

It was not until the nineteenth century that a rigorous foundation for calculus was provided by Augustin Cauchy (1789-1857) and Karl Weierstrass (1815-1897). The essence of their solution to the problem was to dispense with infinitesimals and the infinite altogether, and instead think in terms of relationships between small, but finite, quantities that potentially can be made arbitrarily small. This approach was formalized in the mathematical conception of limit. For example, the sequence of polygons with increasing numbers of sides has the circle as its limit because one can produce a polygon that is arbitrarily close to the circle by selecting the number of sides to be sufficiently large. Thus, although the polygons never actually become the circle, a polygon can be found that is as close as one wants to the circle. Since there is no appeal to infinitesimals or the infinite, this reasoning provides a rigorous foundation for the methods of the calculus. This rigorous foundation for calculus, thus represented a turn back toward the conception of the potential infinite, and an elimination of the actual infinite from calculus.

Yet, a fundamental problem at the basis of both analytic geometry and calculus remained unsolved: how can we justify using irrational numbers that cannot be expressed in finite terms? The solution to this problem was provided by Richard Dedekind (1831-1916) who essentially was forced to formally introduce the infinity of the continuum into mathematics. Because there are points in the geometrical continuum, such as the square root of two, that do not correspond to any rational number, Dedekind devised a technique for filling the ‘gaps’ between rational numbers with the irrational numbers. Dedekind’s definition, however, required the use of infinite sets of rational numbers. Thus, the actual infinite ultimately had to be explicitly affirmed in mathematics in order to provide a foundation for the numbers used in both analytic geometry and calculus.

Georg Cantor (1845-1918) was also instrumental in revitalizing the actual infinite in mathematics. He was the first to provide a rigorous mathematics of transfinite numbers, as well as the first systematic mathematical theory of sets. One of Cantor’s fundamental contributions is a method for comparing the size of infinite sets. According to Cantor’s definition, a first set is equal in size to a second if there is a one-to-one correspondence between their members. For example, the set of even integers is equal in size to the set of odd integers. Less obvious, however, is the fact that the set of even integers is equal in size to the set of all integers: each integer is paired with its double. Even more remarkable was a proof by Cantor that the set of integers is the same size as the set of all rational numbers. Cantor also proved that the set of points in a finite line segment is the same size as the set of points in an infinitely long line. Moreover, the set of points in the finite line segment is also the same size as the set of points in all of three-dimensional space! With the continuum, therefore, an infinite space is completely contained in a finite line segment. One might begin to suspect from these discoveries that all infinite sets are the same size. Surprisingly, however, Cantor proved that the set of points in the continuum of a line is a larger infinity than the infinity of the integers. Thus, there are different degrees of mathematical infinity.

Cantor’s mathematics of the infinite, however, had its own paradoxes. At the basis of Cantor’s theory, and all of modern mathematics, is the intuition of set, which Cantor defined as follows: a set is a many which allows itself to be thought of as a one. Bertrand Russell (1872-1970) soon discovered, however, that even the simple idea of set has inherent paradoxes. Russell viewed these paradoxes as a problem to be eliminated by enforcing a strict linear hierarchy of sets. Cantor, on the other hand, viewed these paradoxes as Cusa might have seen them: Whereas some collections of many things can be consistently thought of as a one, others are so infinitely large that they cannot be consistently thought of as a one. Cantor called these collections inconsistent collections, and regarded them as absolutely infinite. Here we are reminded of Cusa’s teaching that the infinite involves coincident contradictories. It is at this point that the consistent mathematics of the infinite ends and the contradictory metaphysics of the absolute infinite begins. As Cantor said,

The Absolute can only be acknowledged and admitted, never known, not even approximately.[11]

The history of the Infinite thus reveals in both mathematics and philosophy a development of increasingly subtle thought in the form of a dialectical dance around the ineffable and incomprehensible Infinite. First we step toward it, reaching with our intuition beyond the limits of rationality and thought into the realm of the paradoxical. Then we step back, struggling to express our insight within the limited scope of reason. But the Absolute Infinite remains, at the border comprehensibility, inviting us with its paradoxes to once again step forward and transcend the apparent division between finite and Infinite. As Nicholas of Cusa closes his treatise on learned ignorance,

These profound matters should be the subject of all the effort of our human intelligence, so that it may raise itself to that simplicity where contradictories coincide.[12]

Bibliography

Boyer, Carl B. (1949), The History of The Calculus and Its Conceptual Development, (New York: Dover).

Burtt, Edwin A. (1955), The Metaphysical Foundations of Modern Science (Garden City, N.Y.: Doubleday Anchor Books).

Butterfield, Herbert (1957), The Origins of Modern Science 1300-1800, Revised Edition (New York: Macmillan Publishing Co., Inc.).

Hallett, Michael (1984), Cantorian Set Theory and Limitation of Size, (Oxford: Oxford University Press).

Hopkins, Jasper (1985), Nicholas of Cusa on Learned Ignorance: A Translation and an Appreaisal of De Docta Ignorantia, (Minneapolis: The Arthur J. Banning Press).

Morris Kline (1972), Mathematical Thought from Ancient to Modern Times, (Oxford: Oxford University Press)

Moore, A. W. (1990), The Infinite, (London: Routledge).

Nicholas of Cusa (1997), Nicholas of Cusa: Selected Spiritual Writings, H. Lawrence Bond, tr., (New York: Paulist Press).

End Notes

[1] Nicholas of Cusa: Selected Spiritual Writings, p. 28.

[2] Nicholas of Cusa (1997), p. 29.

[3] Hopkins (1985), p. 70.

[4] Hopkins (1985), p. 50.

[5] Hopkins (1985), p. 52.

[6] Nicholas of Cusa (1997), p. 158-159.

[7] Nicholas of Cusa (1997), p. 161.

[8] Nicholas of Cusa (1997), p. 158-159.

[9] Nicholas of Cusa (1997), p. 160.

[10] Kline (1972), p. 251.

[11] Hallett (1984), p. 13.

[12] Nicholas of Cusa (1997), p. 206.

 

Posted in: Uncategorized